Skip to content

VVUQ Patterns

The computing pattern, also called Multiscale Computing Patterns (MCP), is aimed to simplify the implementation of the multiscale application by enhancing the execution of scenarios. From the application’s point of view, a pattern can determine the ordering and composition of single-scale models that are coupled within a multiscale application.

UQP

Uncertainty quantification (UQ) is an increasingly important field in the simulation-based modelling of scientific applications. It can be defined as a bridge between the statistical and probability theory, and computer simulation-based techniques with 'the real world'. In other words, by identifying the source of uncertainty in each component of the model, UQ aims to make the results more reliable and have close predictions of the complex physical systems. A typical UQ problem involves one or more mathematical model subjects to some uncertainty of model parameter value.

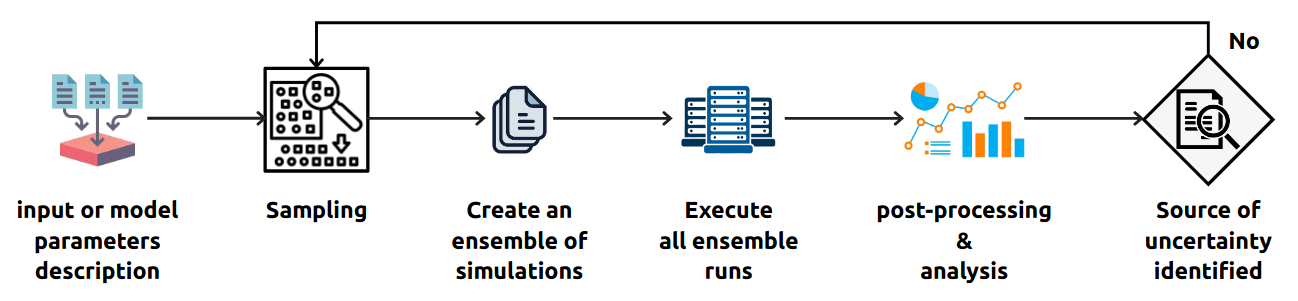Software architecture of the UQ system

Uncertainty Quantification Pattern (UQP) is the term for workflows and algorithms focused on uncertainty quantification and propagation or sensitivity analysis. A general procedure/workflow for UQP can be defined as follows:

  • Create an ensemble of simulations, i.e. individual runs of model simulation executions, containing different input or model parameters for each run;
  • Execute all ensemble runs;
  • Perform post-processing analysis by using statistical techniques, such as the Monte Carlo, Polynomial Chaos and the Stochastic Collocation methods, to measure the error distribution for each input or model parameters (individually);
  • Refine and report the previous steps until the confidence in the simulation results is reached, i.e. identifying the source of uncertainty in the model parameters.

VVP

Verification and validation (V&V) provide a framework for building confidence in computational simulation predictions. The Verification process addresses the quality of the numerical treatment of the model that is used in the prediction, and the validation process addresses the quality of the model. The inclusion of V&V is the key to obtaining credibility of a proposed model. Given the diversity of applications, there is no doubt that having a V&V pattern increases trustworthiness of the simulation model.

Within VECMA project, we identified four prominent V&V patterns which are most suitable for multiscale computing applications:

  1. Stable Intermediate Forms (SIF)
  2. Level of Refinement (LoR)
  3. Ensemble Output Validation (EoV)
  4. Quantities of Interest Distribution Comparison (QDC)

Within FabSim3, we provide support for these V&V patterns as follow:

Level of Refinement (LoR)

ensemble_vvp_LoR function goes through all the output directories and calculates the scores

def ensemble_vvp_LoR(results_dirs_PATH, load_QoIs_function, aggregation_function, **kwargs)
    ...

where

  • results_dirs_PATH: list of result dirs, one directory for each resolution and each one containing the same QoIs stored to disk.
  • load_QoIs_function: a function which loads the QoIs from each subdirectory of the results_dirs_PATH.
  • aggregation_function: function to combine all results

  • **kwargs: The optional input parameter items that will be passed to aggregation_function function.

  • The returned score is in dictionary format and has the following structure: 

    result_dir_1_name:
    order: <polynomial_order>
    runs: <num_runs>
    value:
        vary_param_1: {<sobol_func_name>:<value>}
        ...
        vary_param_X: {<sobol_func_name>:<value>}
...
result_dir_N_name:
      order: <polynomial_order>
      runs: <num_runs>
      value:
            vary_param_1: {<sobol_func_name>:<value>}
            ...
            vary_param_X: {<sobol_func_name>:<value>}

A usage example from the FabFlee plugin

from fabsim.VVP.vvp import ensemble_vvp_LoR
ensemble_vvp_LoR(
    results_dirs_PATH=sobol_work_dir,
    load_QoIs_function=load_QoIs_function,
    aggregation_function=plot_convergence,
    plot_file_path=sobol_work_dir        
)

def load_QoIs_function(result_dir):
    """
    we load input sobols.yml with this structure:
    vary_param_1:
        sobols_first: <array[....]>
        sobols_first_gmean: <value>
        sobols_first_mean: <value>
    ...
    vary_param_N:
        sobols_first: <array[....]>
        sobols_first_gmean: <value>
        sobols_first_mean: <value>
    campaign_info:
        distribution_type: <str>
        name: <str> # name of campaign
        num_runs: <int>
        polynomial_order: <int>
        sampler: <str> # name of sampler
        work_dir: <str> # PATH to this campaign result
    The returns values are : QoIs_values,polynomial_order
        In this implementation, QoIs_values has this
    vary_param_1:
        score: <value>
    ...
    vary_param_N:
        score: <value>
    """
    data_file_name = os.path.join(result_dir, "sobols.yml")
    sobols_data = yaml.load(open(data_file_name), Loader=yaml.SafeLoader)
    polynomial_order = sobols_data["campaign_info"]["polynomial_order"]
    num_runs = sobols_data["campaign_info"]["num_runs"]
    del sobols_data["campaign_info"]

    # sobols_first_mean or sobols_first_gmean
    score_column_name = "sobols_first_mean"

    QoIs_values = {}
    for param in sobols_data:
        QoIs_values.update({param: {}})
        for key in sobols_data[param]:
            if key == score_column_name:
                QoIs_values[param].update({
                    key: sobols_data[param][key]
                })

    return QoIs_values, polynomial_order, num_runs

def plot_convergence(scores, plot_file_path):
    """
    The VVP agregation_function, compares the sobol indices (as function of
    the polynomial order)
    input scores structure:
    result_dir_1_name:
        order: <polynomial_order>
        value:
            vary_param_1: {<sobol_func_name>:<value>}
            ...
            vary_param_z: {<sobol_func_name>:<value>}
    ...
    result_dir_N_name:
        order: <polynomial_order>
        value:
            vary_param_1: {<sobol_func_name>:<value>}
            ...
            vary_param_z: {<sobol_func_name>:<value>}

    ------------------------------------------------------------------
    NOTE: Here, we use the result with maximum polynomial order as the
        reference value
    """
    last_item_key = list(scores)[-1]

    #############################################
    # ref_sobols_value structure:               #
    #                                           #
    # vary_param_1: {<sobol_func_name>:<value>} #
    # ...                                       #
    # vary_param_n: {<sobol_func_name>:<value>} #
    #############################################
    xticks = []
    ref_sobols_value = scores[last_item_key]["value"]

    results = {}
    results.update({"polynomial_order": []})
    compare_res = {}
    for run_dir in scores:
        polynomial_order = scores[run_dir]["order"]
        num_runs = scores[run_dir]["runs"]
        xticks.append("PO={}\nruns={}".format(polynomial_order, num_runs))
        results["polynomial_order"].append(polynomial_order)
        poly_key = "polynomial_order {}".format(polynomial_order)
        compare_res.update({poly_key: {}})
        for param in scores[run_dir]["value"]:
            if param not in results:
                results.update({param: []})
            sb_func_name = list(scores[run_dir]["value"][param].keys())[0]
            sb = scores[run_dir]["value"][param][sb_func_name]
            results[param].append(sb)

    #############################################
    # plotting results                          #
    # results dict structure                    #
    #       vary_param_1: [run1,run2,...]       #
    #       vary_param_2: [run1,run2,...]       #
    #       polynomial_order: [po1,po2,...]     #
    #############################################

    params = list(results.keys())
    params.remove("polynomial_order")

    fig, ax = plt.subplots()
    ax.set_xlabel("Polynomial Order")
    ax.set_ylabel("sobol indices")
    ax.set_title("convergence", fontsize=10, fontweight="bold")

    X = range(len(results["polynomial_order"]))
    for param in params:
        ax.plot(X, results[param], label=param)

    plt.xticks(X, xticks)
    plt.tight_layout()
    plt.legend(loc="best")
    convergence_plot_file_name = "vvp_QoI_convergence.png"
    plt.savefig(os.path.join(plot_file_path, convergence_plot_file_name),
                dpi=400)

    print("=" * 50)
    print("The convergence plot generated ...")
    print(os.path.join(plot_file_path, convergence_plot_file_name))
    print("=" * 50)

In this example, we pass the input arguments plot_file_path=sobol_work_dir to the function. As it mentioned before, all **kwargs variables will be passed to the aggregation_function

Ensemble Output Validation (EoV)

ensemble_vvp function goes through all the output directories and calculates the scores. 

def ensemble_vvp(results_dirs, sample_testing_function, aggregation_function, **kwargs)
    ...

  • results_dirs: list of result dirs to analyse.
  • sample_testing_function: analysis/validation/verification function to be performed on each subdirectory of the results_dirs.
  • aggregation_function: function to combine all results.
  • **kwargs: The optional input parameter items that can be used to give explicit ordering of the various subdirectories.

The ensemble_vvp function returns a dict containing the score per each results_dirs sub-directory.

A usage example from the FabFlee plugin

import fabsim.VVP.vvp as vvp
vvp.ensemble_vvp(
    results_dirs="{}/{}/RUNS".format(env.local_results, results_dir),
    sample_testing_function=vvp_validate_results,
    aggregation_function=make_vvp_mean
)

def vvp_validate_results(output_dir="", **kwargs):
    """ Extract validation results (no dependencies on FabSim env). """

    flee_location_local = user_config["localhost"].get(
        "flee_location", user_config["default"].get("flee_location"))

    local("python3 %s/flee/postprocessing/extract-validation-results.py %s "
          "> %s/validation_results.yml"
          % (flee_location_local, output_dir, output_dir))

    with open("{}/validation_results.yml".format(output_dir), 'r') as val_yaml:
        validation_results = yaml.load(val_yaml, Loader=yaml.SafeLoader)

        # TODO: make a proper validation metric using a validation schema.
        # print(validation_results["totals"]["Error (rescaled)"])
        print("Validation {}: {}".format(output_dir.split("/")[-1],
                                         validation_results["totals"][
                                         "Error (rescaled)"]))
        return validation_results["totals"]["Error (rescaled)"]

    print("error: vvp_validate_results failed on {}".format(output_dir))
    return -1.0

def make_vvp_mean(np_array, **kwargs):
    mean_score = np.mean(np_array)
    print("Mean score: {}".format(mean_score))
    return mean_score

Quantities of Interest Distribution Comparison (QDC)

ensemble_vvp_QoI function goes through all the output directories and calculates several similarity measures. 

def ensemble_vvp_QoI(simulation_result_QoI, uncertainty_result_QoI, QoI_name)
    ...
where

  • simulation_result_QoI : the experimental QoI data.
  • uncertainty_result_QoI : the uncertainty QoI results
  • QoI_name : the name of QoI

In the current implementation, the supported similarity measures are: * Jensen-Shannon divergence * Renyi divergence * Cosine distance * Euclidean distance * Kullback-Leibler divergence

And ensemble_vvp_QoI function returns a dictionary containing calculated similarity measure with the following structure: 

{
    "similarity measure function name":
    {
        "QoI_name" : [similarity_measure_function_result]
    }
}

A usage example from the FabFlee plugin

from fabsim.VVP.vvp import ensemble_vvp_QoI
ensemble_vvp_QoI(
    simulation_result_QoI=sim_result,
    uncertainty_result_QoI=uncertainty_result,
    QoI_name=QoI_name
)

sim_result array contains the simulation results for QoI (here Total Error) column.

uncertainty_result array contains the results for QoI (here Total Error) with uncertainty.

QoI_name is the name of target QoI.